- 参考资料
- 《数据结构与算法JavaScript描述》
- 《学习JavaScript数据结构与算法》
一、树的简介
- 树是计算机科学中经常用到的一种数据结构。
- 树是一种非线性的数据结构,以分层的方式存储数据。
- 树被用来存储具有层级关系的数据,比如文件系统中的文件;树还被用来存储有序列表。
二、树的相关术语
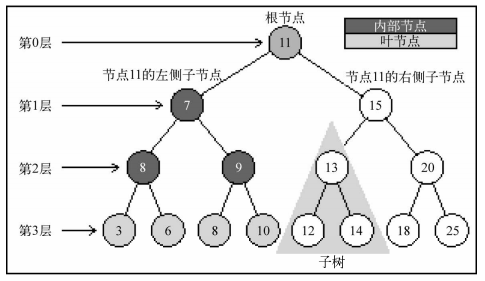
- 根节点:位于树顶部的节点就是根节点(“11”就是根节点)
- 根节点没有父节点
- 树中的每个元素都叫做节点,节点分为内部节点和外部节点
- 内部节点:至少有一个子节点的节点称为内部节点(“7”就是外部节点)
- 外部节点:没有子元素的节点称为外部节点或叶节点(第3层的都是叶节点)
- 子树:子树由节点和它的后代构成。(节点“13”、“12”和“14”构成了上图中树的一棵子树)
- 树的深度:节点的深度取决于它的祖先节点的数量。
- 例如:节点“3”有3个祖先节点(“5”、“7”和“11”),它的深度为3。
- 树的高度:树的高度取决于所有节点深度的最大值。
- 上图中的树的高度为3(最大高度已在图中表示——第3层)。
三、二叉树和二叉搜索树
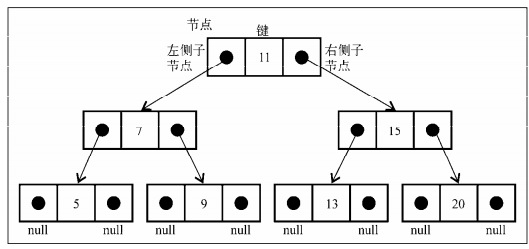
- 二叉树中的节点最多只能有两个子节点:一个是左侧子节点,另一个是右侧子节点。
- 这些定义有助于我们写出更高效的向/从树中插入、查找和删除节点的算法。
- 二叉搜索树(
BST)是二叉树的一种,但是它只允许你在左侧节点存储(比父节点)小的值, 在右侧节点存储(比父节点)大(或者等于)的值。
四、实现二叉搜索树
4.1 创建二叉搜索树
- 思路
- 判断根节点是否存在,不存在,那么添加的节点则作为根节点
- 设置根节点作为当前节点
- 如果需要添加的节点 小于 当前节点,则设置新的当前节点为原节点的左节点;反之,执行第5步
- 如果当前节点的左节点为 null,就将新节点插入到这个位置,并且退出循环;反之,执行下一次循环
- 设置新的当前节点为原节点的右节点
- 如果当前节点的右节点为 null,就将新节点插入到这个位置,并且退出循环;反之,执行下一次循环
- 添加节点 - 法1 (循环),demo
/**
* 添加节点
* @param data
*/
BinarySearchTree.prototype.insert = function (data) {
const newNode = new Node(data)
if (!this.root) {
this.root = newNode
} else {
let currentNode = this.root
let parentNode = null
while (true) {
parentNode = currentNode
if (data < currentNode.data) {
currentNode = currentNode.left
if (currentNode === null) {
parentNode.left = newNode
break
}
} else {
currentNode = currentNode.right
if (currentNode === null) {
parentNode.right = newNode
break
}
}
}
}
}
- 添加节点 - 法2 (递归),demo
/**
* 添加节点
* @param data
*/
BinarySearchTree.prototype.insert = function (data) {
const newNode = new Node(data)
if (!this.root) {
this.root = newNode
} else {
insertNode(this.root, newNode)
}
}
/**
* 辅助函数:插入节点
* @param node
* @param newNode
*/
function insertNode (node, newNode) {
if (newNode.data < node.data) {
if (node.left === null) {
node.left = newNode
} else {
insertNode(node.left, newNode)
}
} else {
if (node.right === null) {
node.right = newNode
} else {
insertNode(node.right, newNode)
}
}
}
4.2 树的遍历
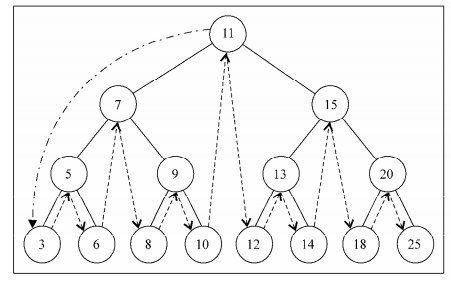
- 中序遍历:从最小到最大的顺序访问所有节点
- 访问的顺序是:访问左侧子节点 ===》 访问节点本身 ===》 访问右侧子节点
/**
* 辅助函数:中序遍历
* @param node
* @param callback
*/
function inOrderTraverseNode (node, callback) {
if (node !== null) {
inOrderTraverseNode(node.left, callback)
callback(node)
inOrderTraverseNode(node.right, callback)
}
}
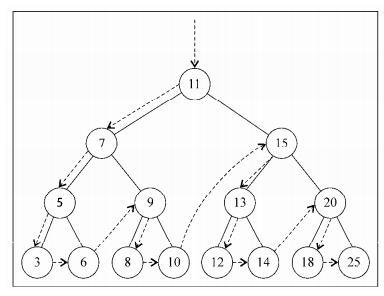
- 先序遍历:
- 访问的顺序是:访问节点本身 ===》 访问左侧子节点 ===》 访问右侧子节点
/**
* 辅助函数:先序遍历
* @param node
* @param callback
*/
function preOrderTraverseNode (node, callback) {
if (node !== null) {
callback(node)
preOrderTraverseNode(node.left, callback)
preOrderTraverseNode(node.right, callback)
}
}
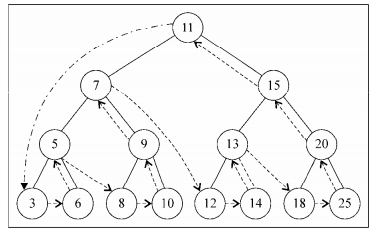
- 后序遍历:
- 访问的顺序是:访问节点的后代节点(从左到右) ===》 访问节点的本身
/**
* 辅助函数:后序遍历
* @param node
* @param callback
*/
function postOrderTraverseNode (node, callback) {
if (node !== null) {
postOrderTraverseNode(node.left, callback)
postOrderTraverseNode(node.right, callback)
callback(node)
}
}
4.3 搜索最小值和最大值
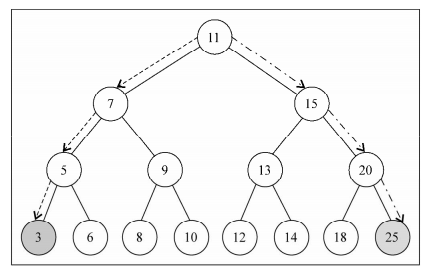
- 最小值:二叉搜索树底部最左的节点
- 最大值:二叉搜索树底部最右的节点
/**
* 辅助函数:获取最小值
* @param node
* @return {*}
*/
function getMin (node) {
if (node) {
while (node && node.left !== null) {
node = node.left
}
return node
}
return null
}
/**
* 辅助函数:获取最大值
* @param node
* @return {*}
*/
function getMax (node) {
if (node) {
while (node && node.right !== null) {
node = node.right
}
return node
}
return null
}
4.4 搜索特定的值
- 思路:
- 如果直接判断找到对应的值,就直接返回这个节点
- 否则,判断要找的值的节点是属于左子树还是右子树,继续查询
- 最终找不到对应的节点,直接返回
null
/**
* 获取特定值
*/
BinarySearchTree.prototype.search = function (data) {
let current = this.root
while (current !== null) {
if (current.data === data) {
return current
}
// 左子树
else if (data < current.data) {
current = current.left
}
// 右子树
else {
current = current.right
}
}
return null
}
4.5 删除节点
/**
* 辅助函数:移除节点
* @param node
* @param data
*/
function removeNode (node, data) {
// 参数node不存在
if (node === null) {
return null
}
// 左子树:data < node.data
if (data < node.data) {
node.left = removeNode(node.left, data)
return node
}
// 右子树:data > node.data
else if (data > node.data) {
node.right = removeNode(node.right, data)
return node
}
// data = node.data
else {
// 有三种情况:
// 1. 移除一个叶节点
if (node.left === null && node.right === null) {
node = null
return node
}
// 2. 移除有一个左侧或右侧子节点的节点
// 移除有一个右侧子节点的节点
if (node.left === null) {
// 右侧子节点替换要删除的节点
node = node.right
return node
}
// 移除有一个左侧子节点的节点
else if (node.right === null) {
// 左侧子节点替换要删除的节点
node = node.left
return node
}
// 3. 移除有两个子节点的节点
// 找到要删除的节点的右子树中最小的节点
// 用这个最小节点的值替换要删除的节点的值
// 由于一棵树不能有相同键的节点
// 因此,替换后,这个最小节点要删除掉
const minNode = getMin(node.right)
node.data = minNode.data
node.right = removeNode(node.right, minNode.data)
return node
}
}
- 大的有4种情况:
- 参数
node不存在,直接返回null- 左子树:
data < node.data- 右子树:
data > node.data- 找到要删除的节点:
data = node.data
- 上述第4点又分为3类
- 第一类:删除的节点是叶节点(即没有子节点)
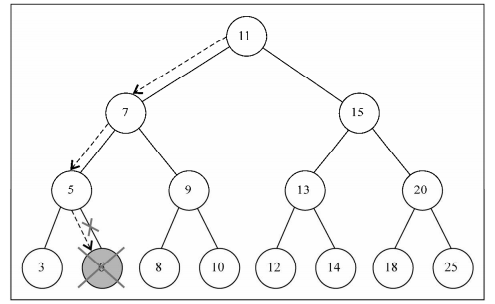
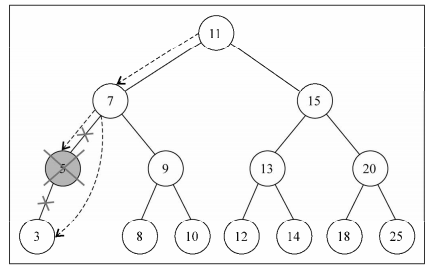
- 第二类:删除有一个左侧或右侧子节点的节点
- 右侧子节点替换要删除的节点 或者 左侧子节点替换要删除的节点
- 记得返回引用
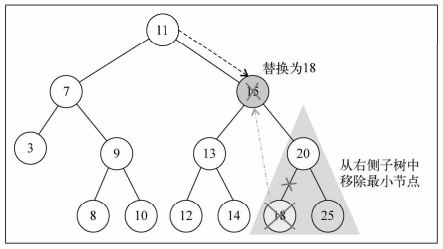
- 第三类:删除有两个子节点的节点
- 找到要删除的节点的右子树中最小的节点
- 用这个最小节点的值替换要删除的节点的值
- 由于一棵树不能有相同键的节点
- 因此,替换后,这个最小节点要删除掉
- 大家看代码的时候,可能都会发现基本每一个
if分支都有一个return语句
- 删除的节点是叶节点:其作用是通过返回
null来将对应的父节点指针赋予null值- 删除有一个左侧或右侧子节点的节点:把对要删除的节点的引用改为对要删除的节点的左侧子节点或者右侧子节点的引用
- 删除有两个子节点的节点:返回新的右侧子节点的引用
